Лаборатория устойчивости и управления
Архивная страница. Лаборатория в 2023 г. присоединена к лаборатории механики сплошной среды.
|

|
Заведующий лабораторией
Маликов Александр Иванович, доктор физ.-мат. наук, профессор, в.н.с.,
профессор Казанского национального исследовательского университета им. А.Н.Туполева.
(843)231-03-00 (КНИТУ-КАИ)
|
|
Сотрудники лаборатории
Основные направления исследований
Исследование систем управления с неопределенными возмущениями, параметрическими и структурными изменениями. Разработка и обоснование методов исследования динамики, оценивания состояния и синтеза систем управления.
Моделирование дрейфа и фокусировки частиц аэрозоля в волновых полях резонаторов с учетом акустических течений.
Методы исследования: принцип редукции с матричными функциями сравнения, квадратичные функции Ляпунова, дифференциальные линейные матричные неравенства.
Лаборатория участвует в выполнении проектов по программам фундаментальных исследований Президиума РАН, гранта РНФ.
Результаты последних лет (2016-2019 гг.)
С применение матричных систем сравнения и дифференциальных линейных матричных неравенств получены условия устойчивости и ограниченности на конечном интервале для класса неавтономных нелинейных систем при учете изменений параметров режима.
Предложены способы оценивания состояния в виде инвариантных эллипсоидов, ограничивающих состояния или выход в каждый момент времени нелинейных неавтономных систем с учетом неопределенных ограниченных возмущений и изменений режимов. Они основаны на получении частных решений матричной системы сравнения или на численном решении дифференциальных линейных матричных неравенств с оптимизацией на каждом шаге дискретизации следа матрицы эллипсоида, ограничивающих состояния или выход.
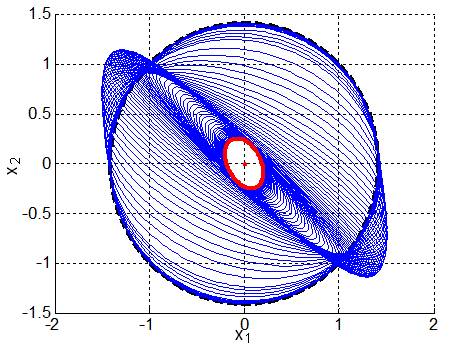
|
Рис. 1. Оценивания состояния в виде эволюционирующего инвариантного эллипсоида для нелинейной модели динамики манипулятора (см. рис. 2) при действии неопределенных ограниченных возмущений
|
Разработаны способы и алгоритмы синтеза переключаемого управления по состоянию для многорежимных объектов, обеспечивающего на конечном интервале ограниченность относительно заданных множеств начальных отклонений и допустимых состояний нелинейной системы.
Разработаны способы и алгоритмы оценивания неопределенных внешних возмущений и диагностических параметров, способов и алгоритмов обнаружения отказов нелинейных систем управления. Предлагаемый подход, основанный на способах синтеза наблюдателей состояния и неизвестных входов, дает возможность успешно диагностировать возникающие неисправности при наличии в системе как неопределенных возмущений, так и погрешностей измерений. Результаты применены для диагностирования датчиков и привода робота манипулятора с нежестким соединением звеньев.
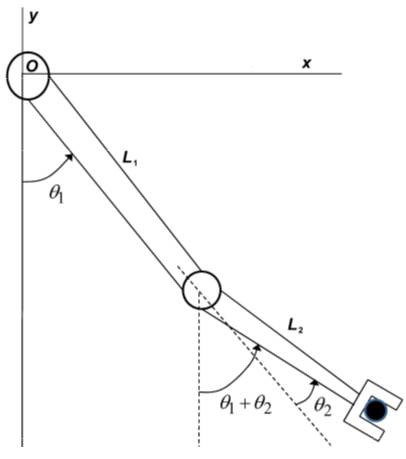
|
Рис. 2. Кинематическая схема манипулятора с двумя звеньями с нежестким соединением и с одним приводом на оси первого звена
|
Разработаны способы синтеза децентрализованных наблюдателей для гарантированного оценивания состояния, способов и алгоритмов синтеза локальных регуляторов, обеспечивающих устойчивость или ограниченность на конечном интервале для заданного режима функционирования при учете неопределенных возмущений, нелинейностей и информационных ограничениях.
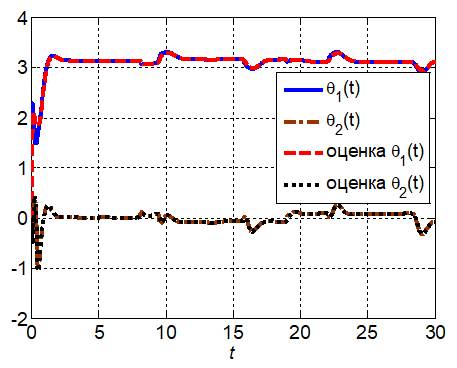
|
Рис. 3. Изменение координат состояния (углов θ1, θ2 ) и их оценки, полученные с помощью наблюдателя, при стабилизации манипулятора в верхнем положении с помощью комбинированного регулятора при действии неопределенных возмущений и неизвестных моментов сопротивления
|
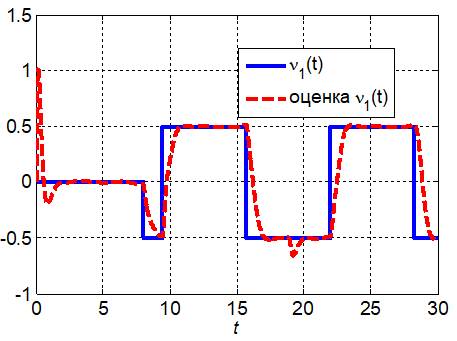
|
Рис. 4. Изменение дополнительного момента сопротивления на оси первого звена манипулятора и его оценка, полученная с помощью наблюдателя состояния и неизвестных входных воздействий
|
Разработаны методы, алгоритмы и программы для моделирования дрейфа и фокусировки частиц в двумерных резонаторах сложной формы. Определены условия существования акустических ловушек - зон повышенной концентрации частиц. Установлено возникновение вихрей Шлихтинга и вихрей Рэлея. Исследовано влияние акустического течения на динамику аэрозольных частиц. Выполнен расчет акустических течений в цилиндрическом, крестообразном и гиперболическом резонаторах с учетом тонких пограничных слоев.
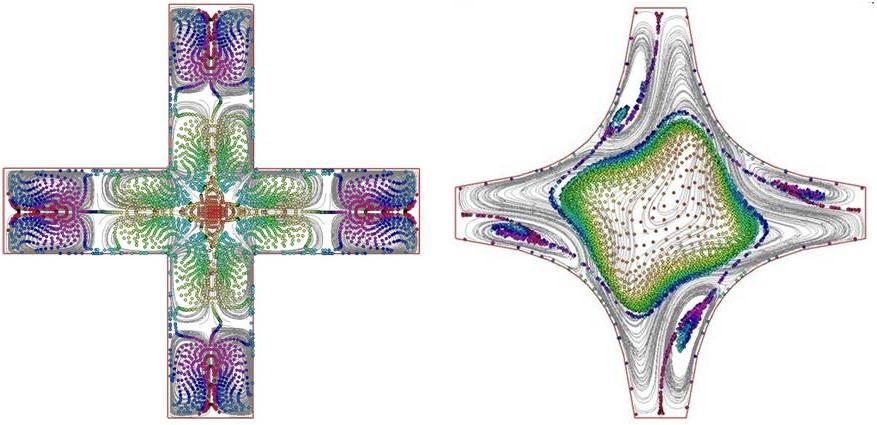 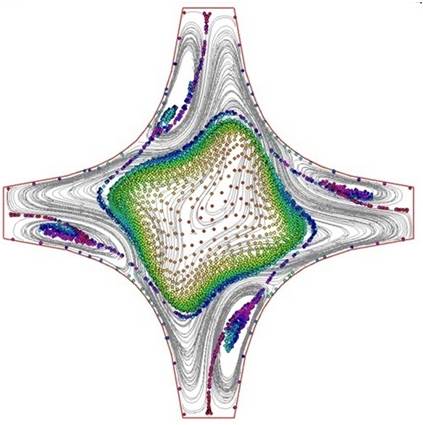
Рис. 5. Линии тока и распределение частиц в крестообразном и гиперболическом резонаторах
Основные публикации
- Vector Lyapunov Functions in Stability Theory / R.Z.Abdyllin, L.J.Anapolski, R.I.Kozlov, A.I.Malikov, V.M.Matrosov, A.A.Voronov, A.S.Zemljakov. - Advanced series in mathematical science and engineering. - World Federation Publisher Company. - 1996. -394 p.
- Осипов П. П. Задачи переноса при свободномолекулярном течении газа и лучистом теплообмене. Казань: Изд-во Казан. гос. техн. ун-та. 2004. 80 с.
- Губайдуллин Д.А., Осипов П.П., Закиров А.Н. Диаграммы направления дрейфа частицы в стоячей волне с учетом силы Бассэ // Инженерно-физический журнал, 2015. Т. 88. № 3. С. 601 - 608.
- Губайдуллин Д.А., Осипов П.П., Закиров А.Н. Влияние силы Бассэ на направление дрейфа включения в стоячей волне // Известия вузов. Проблемы энергетики, 2015. № 1-2. С. 133 - 139.
- Маликов А.И. Оценивание состояния и стабилизация дискретных систем с секторными нелинейностями и возмущениями // Вестник КГТУ им. А.Н.Туполева, 2015. № 1. С. 131 - 141.
- Isankin M.A., Malikov A.I. The Analysis of Dynamic and Stabilization at Uncertain Perturbations of the Two Link Manipulator with Non-Rigid Connection // Proceedings of 2016 International Conference "Stability and Oscillations of Nonlinear Control Systems" (Pyatnitskiy's Conference). IEEE Xplore. 2016. P.1–4.
- Исанькин М.А., Маликов А.И. Синтез управления по состоянию наблюдателя робота манипулятора с двумя звеньями с нежестким соединением // Вестник КГТУ им. А.Н.Туполева, 2016. № 3. С. 112 - 121.
- Маликов А.И. Синтез наблюдателей состояния для нелинейных липшицевых систем с неопределенными ограниченными по Lоо норме возмущениями // Вестник КГТУ им. А.Н.Туполева, 2016. № 3. С. 128 - 140.
- Губайдуллин Д.А., Осипов П.П., Насыров Р.Р. Влияние положения частицы и коэффициента увлечения на скорость дрейфа в акустическом резонаторе // Инженерно-физический журнал, 2016. Т. 89. № 2. С. 400 - 404.
- Маликов А.И. Оценивание состояния и стабилизация непрерывных систем с неопределенными нелинейностями и возмущениями // Автоматика и телемеханика, 2016. № 5. С. 19 - 36.
- Маликов А.И. Управление на конечном интервале нелинейных систем одного класса с H∞- критерием качества // Известия РАН. Теория и системы управления, 2017. № 3. С. 25 - 46.
- Malikov A.I. State and Unknown Inputs Finite Time Estimation for Time-Varying Nonlinear Lipschitz Systems with Uncertain Disturbances // Preprints of the 20th World Congress The International Federation of Automatic Control. Toulouse, France, July 9-14, 2017. P. 1475-1480 // IFAC PapersOnLine 2017. V. 50. Is. 1. P. 1439–1444.
- Губайдуллин Д.А., Осипов П.П., Альмакаев И.М. Моделирование дрейфа мелкодисперсных частиц в акустическом резонаторе с помощью пакета CFD // Известия вузов. Проблемы энергетики, 2017. Т. 19. № 9-10. С. 112 - 121.
- Федяев В.Л., Осипов П.П. , Беляев А.В., Сироткина Л.В. Аналитические оценки теплопереноса при электроконтактной сварке // Вестник КГТУ им. А.Н.Туполева, 2017. Т. 2. С. 97 - 101.
- Федяев В.Л., Осипов П.П. , Беляев А.В., Сироткина А.В. Математическое моделирование процессов, протекающих при электроконтактной сварке деталей с покрытиями // Научно- технические ведомости СПбПУ. Естественные и инженерные науки, 2017. Т. 23. № 4. С. 149 - 158.
- Маликов А.И. Синтез наблюдателей состояния по результатам измерений для нелинейных липшицевых систем с неопределенными возмущениями // Автоматика и телемеханика, 2017. № 5. С. 16 - 35.
- Маликов А.И. Синтез децентрализованных наблюдателей для нелинейных многосвязных систем с неопределенными ограниченными по L2-норме возмущениями // Вестник КГТУ им. А.Н.Туполева, 2018. № 3. С. 162 - 171.
- Акбиров Р.Р., Маликов А.И. Управление двойным перевернутым маятником на тележке // Вестник КГТУ им. А.Н.Туполева, 2018. Т. 74. № 2. С. 168 - 177.
- Маликов А.И. Синтез децентрализованного управления по состоянию наблюдателя для нелинейных многосвязных систем с неопределенными возмущениями // Вестник КГТУ им. А.Н.Туполева, 2018. № 4. С. 242 - 254.
- Губайдуллин Д.А., Осипов П.П., Насыров Р.Р. Влияние коэффициента увлечения частиц на их распределение в двумерном акустическом резонаторе // Инженерно-физический журнал, 2018. Т. 91. № 3. С. 734 - 742.
- Gubaidullin D.A., Ossipov P.P., Abdyushev A.A. Simulation of aerosol distribution in hyperbolic resonator // Applied Mathematical Modelling, 2018. № 62. С. 181 - 193.
- Маликов А.И. Синтез наблюдателей состояния и неизвестных входов для нелинейных липшицевых систем с неопределенными возмущениями // Автоматика и телемеханика, 2018. № 3. С. 21 - 43.
- Федяев В.Л., Осипов П.П. , Беляев А.В., Сироткина Л.В. Нагрев и плавление насыпных кусковых материалов // Вестник Самарского университета. Аэрокосм. техника, технологии и машиностроение, 2018. Т. 17. № 2. С. 174 - 182.
- Osipov P. P., and I. M. Almakaev Simulation of particles drift and acoustic streaming of polythropic viscous gas in a closed tube // Lobachevskii Journal of Mathematics, 2019. Т. 40. № 6. С. 802 - 807.
- Маликов А.И. Оценивание состояния и стабилизация дискретных систем с неопределенными нелинейностями и возмущениями // Автоматика и телемеханика, 2019. № 11. С. 59 - 82.
- Malikov A.I. State and unknown input observers for time-varying nonlinear systems with uncertain disturbances // Lobachevskii Journal of Mathematics, 2019. Т. 40. № 6. С. 769 - 775.
- Губайдуллин Д.А., Осипов П.П. Аэрогидродинамика дисперсной частицы // М.: Физматлит, 2020. 176 с. ISBN: 978-5-9221-1883-5
- Osipov P.P., Nasyrov R.R. Resonance curve in a rectangular closed channel // Lobachevskii Journal of Mathematics, 2020. Т. 41. № 7. С. 1283 - 1288.
- Gubaidullin D.A., Osipov P.P., Nasyrov R.R. Particle drift at rotational oscillations of the lower boundary of a rectangular resonator // Journal of Physics: Conference series, 1588, 012041, 2020. 3 с.
- Gubaidullin D.A., Osipov P.P., Nasyrov R.R. Threshold frequency of standing wave at hydrodynamic separation of particles // Journal of Physics: Conference series, 1588, 012040, 2020. 5 с.
- Malikov A.I. Observer based control for time-varying nonlinear systems with uncertain disturbances and unknown inputs // Lobachevskii Journal of Mathematics, 2020. Т. 41. № 7. С. 1248 - 1254.
Ранее в лаборатории проводились также исследования в области релятивистской динамики сосредоточенной переменной массы покоя.
|



