Лаборатория вычислительной динамики сплошной среды
ВОЗДЕЙСТВИЕ КАВИТАЦИИ НА ТЕЛО
АКТУАЛЬНОСТЬ ПРОБЛЕМЫ
Разрушение:
- лопастей гребных винтов водных двигателей
- водных крыльев
- лопаток гидротурбин
- лопастей проточных частей гидронасосов
- проточных каналов гидродвигателей
- клапанов в устройствах пневмоавтоматики
- элементов проточных частей теплообменников
- трубопроводных систем транспортировки жидкостей
- деталей топливной аппаратуры
- побочное разрушение органических тканей в лазерной микрохирургии
- усиление разрушений подводных и надводных объектов при подводных взрывах
- шум, вибрации
- снижение эффективности работы устройств
Примеры разрушительного воздействия кавитации

Водослив ГЭС (диаметр 15.2 м)
[Brennen C.E. Hydrodynamics of Pumps,Oxford University Press.1994. 293 p].

|
Кавитационное разрушение крыльчатки водяного насоса
[Tash H.A., Sadeghi M., Shervanitabar M.T., Ettefagh M.M., The Application of Laser Velocity Meter in De-tecting Incipient Cavitation and Measurement its Intensity, Inside Axial Flow Pumps // Journal of Applied Sci-ences. 2009. V.9(7). P. 1317-1323 ]
|

Лопасти гидротурбины

Вращающиеся детали гидронасосов
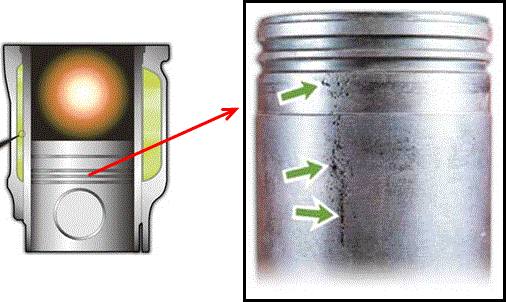
Гильза цилиндра двигателя
Применение
- интенсификация химических реакций, процессов гомогенизации, перемешивания, синтез наноалмазов
- диагностика, доставка лекарственных препаратов в органы, ткани и клетки, удаление камней в почках, желчном пузыре
- гомогенизация топлива, получение качественных дисперсионно-топливных систем, улучшение качества бетона, очистка труб и поверхностей
- гомогенизация, экстрагирование, эмульгирование, пастеризация в производстве продуктов питания,
- обработка нефти перед транспортировкой и крекингом, очистка от отложений стенок скважин, насосно-компрессорных труб, систем транспортировки нефти.
Примеры применения кавитации
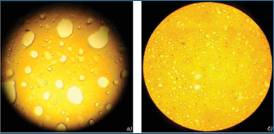
Обработка водомазутной смеси
[Геллер C.В. Приготовление водомазутных эмульсий
посредством волновой диспергации
//Новости теплоснабжения.- 2010 г., №04 (116) 2010 г. ]

Эмульгирование

Очистка деталей сложной формы (фильтров)
РЕЗУЛЬТАТЫ
1. Разработана методика численного исследования ударного воздействия пузырьков на тело, состоящая из трех этапов [1, 6, 11]. На первом этапе методом граничных элементов рассчитывается форма пузырька и кумулятивной струи, поля скоростей и давлений в жидкости. На втором этапе в предположении абсолютной твердости тела и без учета вязкости жидкости (это соответствует достаточно большим пузырькам и телам, по свойствам близким к металлическим) рассчитывается ударно-волновая динамика в струе и окружающем газе. Результатом второго этапа является дискретная динамическая нагрузка на поверхности тела в ходе удара струи. Далее эта нагрузка аппроксимируется сплайнами и аналитическими зависимостями. На третьем этапе полученная аппроксимация нагрузки используется для расчета деформаций поверхности тела и полей напряжения в приповерхностном слое.
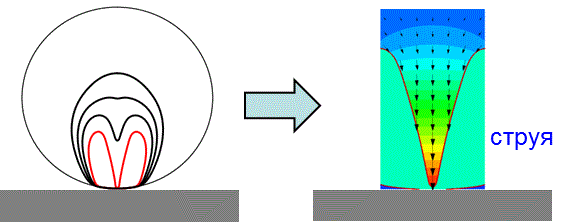 Этап 1. Расчет сжатия пузырька у стенки. Этап 1. Расчет сжатия пузырька у стенки.
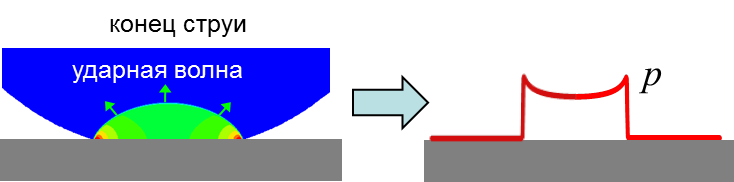 Этап 2. Расчет ударной нагрузки на стенку. Этап 2. Расчет ударной нагрузки на стенку.
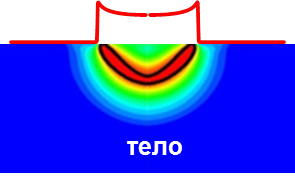 Этап 3. Расчет воздействия ударной нагрузки на тело. Этап 3. Расчет воздействия ударной нагрузки на тело.
Рис.1. Методика расчета ударного воздействия пузырьков на тело.
2. Разработаны алгоритмы расчета осесимметричного сжатия сфероидального кавитационного пузырька в идеальной несжимаемой жидкости вблизи плоской твердой стенки. Методика основана на шаговом методе для отслеживания движения контура во времени и методе граничных элементов. При этом процесс схлопывания пузырька делится на два временных периода. Первый продолжается до момента удара возникающей при сжатии кумулятивной струи по противоположной стороне поверхности пузырька, второй включает в себя фазу движения тороидального пузырька, образованного в результате этого удара. Выполнено сравнение с численными и экспериментальными результатами других авторов и получено их хорошее совпадение [4, 7].

|
Рис.2. Сжатие пузырька у стенки в условиях экспериментов [Philipp A., Lauterborn W. Cavitation erosion by single laser-produced bubbles // J. Fluid Mech. 1998. V. 361. P. 75–116] до начала тороидальной фазы движения (a) и один из моментов сжатия в условиях экспериментов [Tong R.P., Schiffers W.P., et. al. The role of `splashing' in the collapse of a laser-generated cavity near a rigid boundary // J. Fluid Mech. 1999. V. 380. P. 339-361 ] на тороидальной фазе движения (b). Верхний ряд – эксперимент, нижний – расчет по разработанной методике.
|
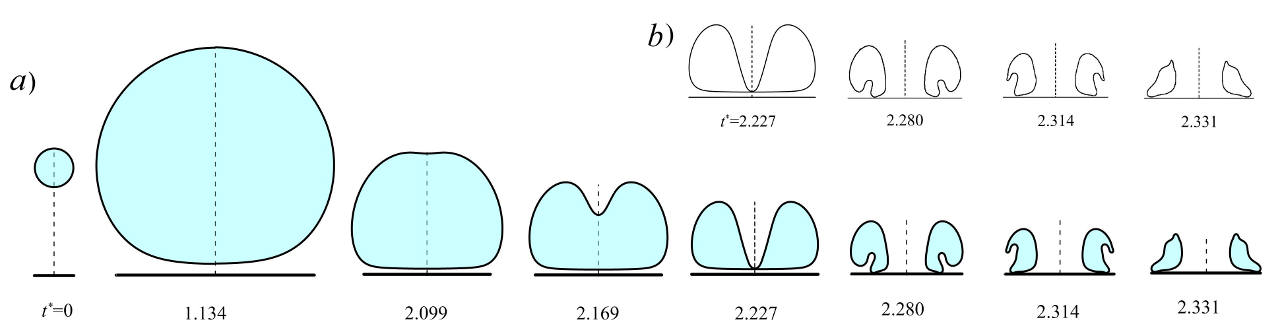
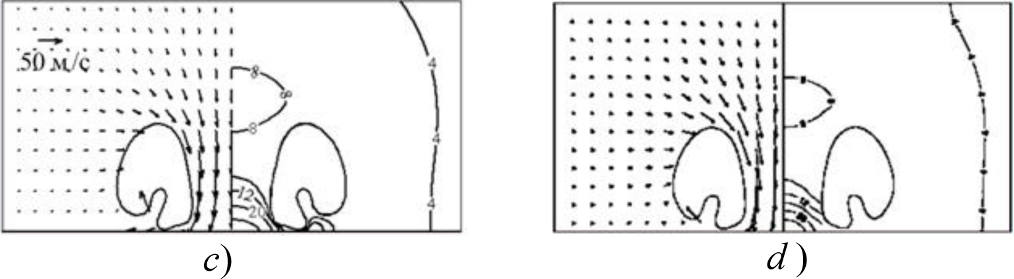
|
Рис.3. Расширение-сжатие пузырька в воде вблизи стенки в условиях расчетов [Tong R.P., Schiffers W.P., et. al. The role of `splashing' in the collapse of a laser-generated cavity near a rigid boundary // J. Fluid Mech. 1999. V. 380. P. 339-361]. Формы пузырьков в последовательные моменты времени, поля давления и скорости жидкости в окрестности пузырька в один из моментов сжатия: a), c) – результаты по созданной методике, b), d) – результаты [Tong R.P., Schiffers W.P., et. al. The role of `splashing' in the collapse of a laser-generated cavity near a rigid boundary // J. Fluid Mech. 1999. V. 380. P. 339-361].
|
3. Изучено влияние на динамику пузырька начального расстояния до стенки и отклонения формы пузырька от сферической. Установлено, что при малой начальной несферичности у пузырька, примыкающего к стенке или удаленного от нее на расстояние, не превышающее половины среднего по объему начального радиуса пузырька, образуется кумулятивная струя, направленная к стенке. При этом с увеличением начального расстояния до стенки у сплюснутого пузырька возрастает скорость соударения конца струи с противоположной ей частью поверхности пузырька, а у вытянутого - давление внутри пузырька [8, 9].
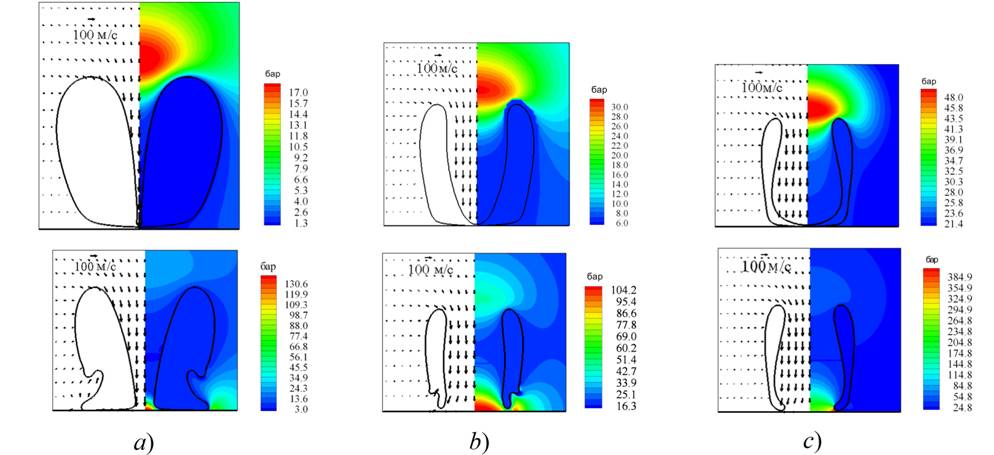
|
Рис.4. Поля скорости и давления в жидкости и формы пузырьков при их сжатии: верхний ряд - в момент удара кумулятивной струи по стенке, нижний ряд - в один из моментов развитой тороидальной фазы движения для изначально слегка сплюснутого е=0.9 (а), сферического е=1 (b) и слегка вытянутого е=1.04 (с) пузырьков; е – отношение полуосей сфероида.
|
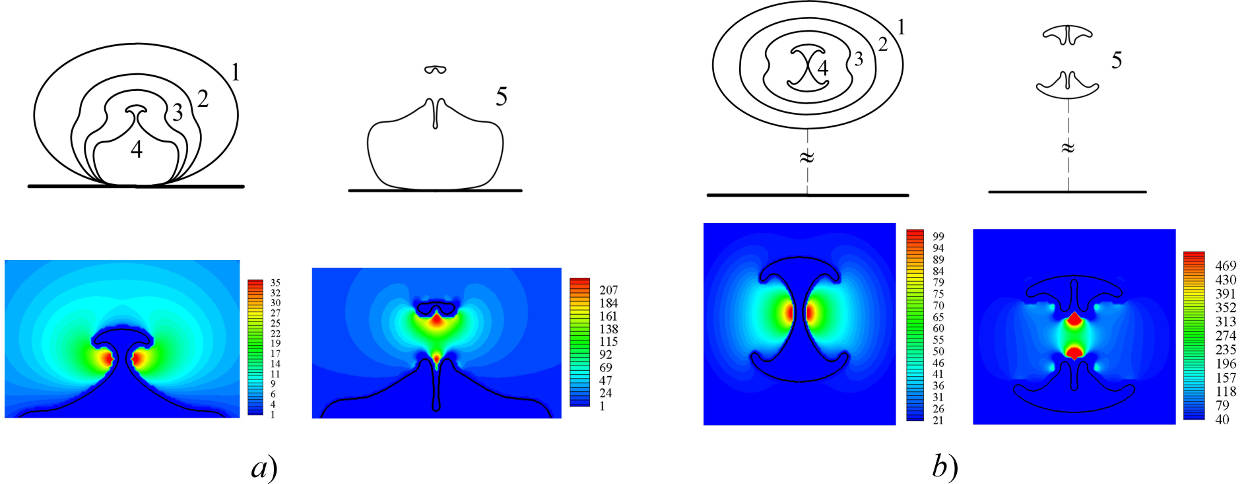
4. Методика расчета сжатия кавитационного пузырька вблизи твердой стенки обобщена на случай его распада на отдельные фрагменты [5].
|
Рис.5. Сжатие пузырька у стенки в двух случаях его распада на отдельные фрагменты: a) – пузырек касается стенки, b) – находится от нее на некотором удалении. Верхний ряд - формы пузырьков в пять моментов времени, нижний ряд - поля давления (бар) в моменты 4, 5.
|
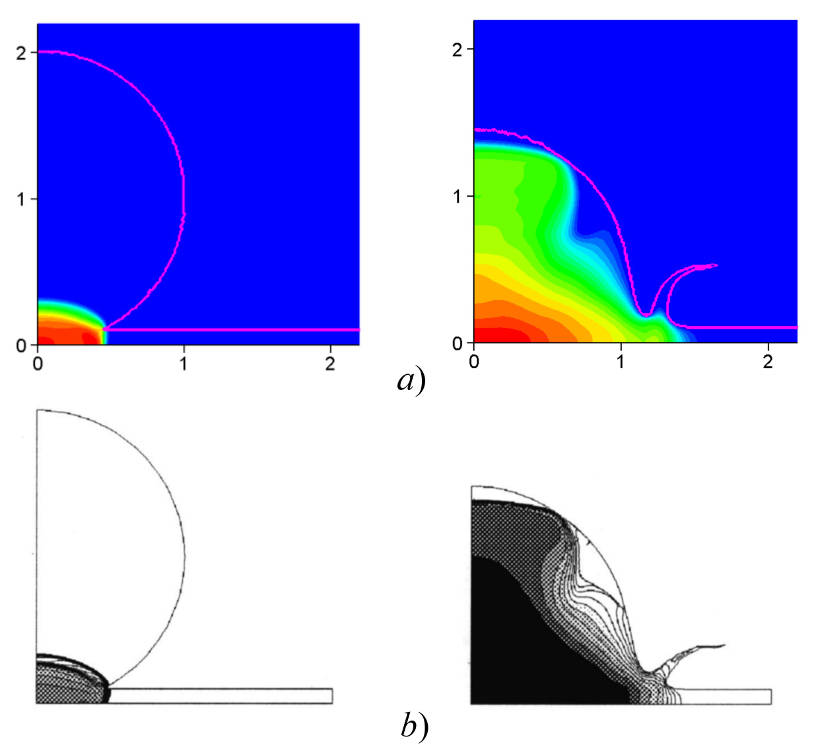
5. Разработаны алгоритмы расчета ударно-волновых процессов в сжимаемых средах с подвижной деформирующейся межфазной границей, в том числе типа газ-жидкость [10-22]. Применяется подход без явного выделения межфазной границы. Для сквозного интегрирования уравнений газовой динамики применяется метод CIP-CUP (Yabe T., Wang P.Y. Unified numerical procedure for compressible and incompressible fluid // J. Phys. Soc. Japan. 1991. V. 60. N. 7. P. 2105–2108). Используется адаптивная сетка специального вида (soroban-сетка, Takizawa K., et. al. Computation of free–surface flows and fluid–object interactions with the CIP method based on adaptive meshless Soroban grids // Comput. Mech. 2007. V.40. P. 167–183), которая представляет собой адаптирующийся к особенностям решения набор узлов на параллельных направляющих линиях.
|
Рис.6. Высокоскоростной удар капли по жидкой прослойке на стенке: a) – результаты расчета по созданной методике, b) – из работы Чижов А. В., Шмидт А. А. Высокоскоростной удар капли о преграду // ЖТФ. 2000. Т. 170. Вып. 12. С.18–27.
|
6. Исследована начальная стадия ударного воздействия высокоскоростной струи на жесткую стенку с прослойкой жидкости [6, 10]. Струя образуется при сжатии слегка сплюснутого микронного кавитационного пузырька у стенки при комнатных условиях, скорость струи 250 м/c. Установлено, что
- если пузырек касается стенки, то давление на стенке неоднородно с минимумом в центре удара и максимумом на периферии (более чем в 3 раза превышающим давление гидроудара).
- при наличии между пузырьком и стенкой жидкого слоя толщиной меньше 0.03 радиуса струи распределение давления на стенке также имеет вышеописанный характер с максимумом, также превышающим давление гидроудара.
- Для прослоек большей толщины давление на стенке распределено почти однородно и не превышает давления гидроудара.
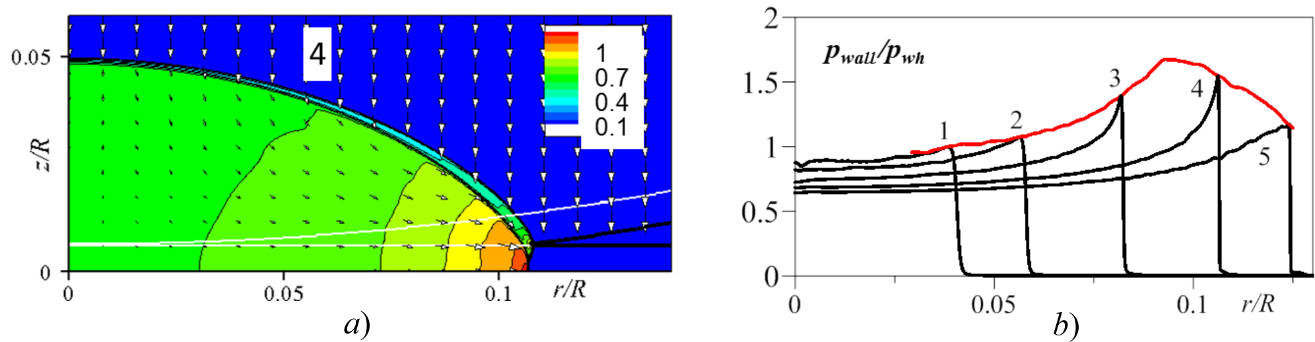
|
Рис.7. Ударное воздействие высокоскоростной струи на жесткую стенку с прослойкой жидкости толщиной d=0.0063R (R – радиус струи): a) – изолинии давления p /pwh (pwh = 5 кбар) и векторы скорости в малой окрестности области контакта струи и прослойки (черные жирные линии – межфазная поверхность, белые линии – ее начальное положение), b) – радиальные профили давления на поверхности стенки в 5 моментов времени и огибающая их максимумов (красная кривая). a) соответствует моменту 4 на b).
|
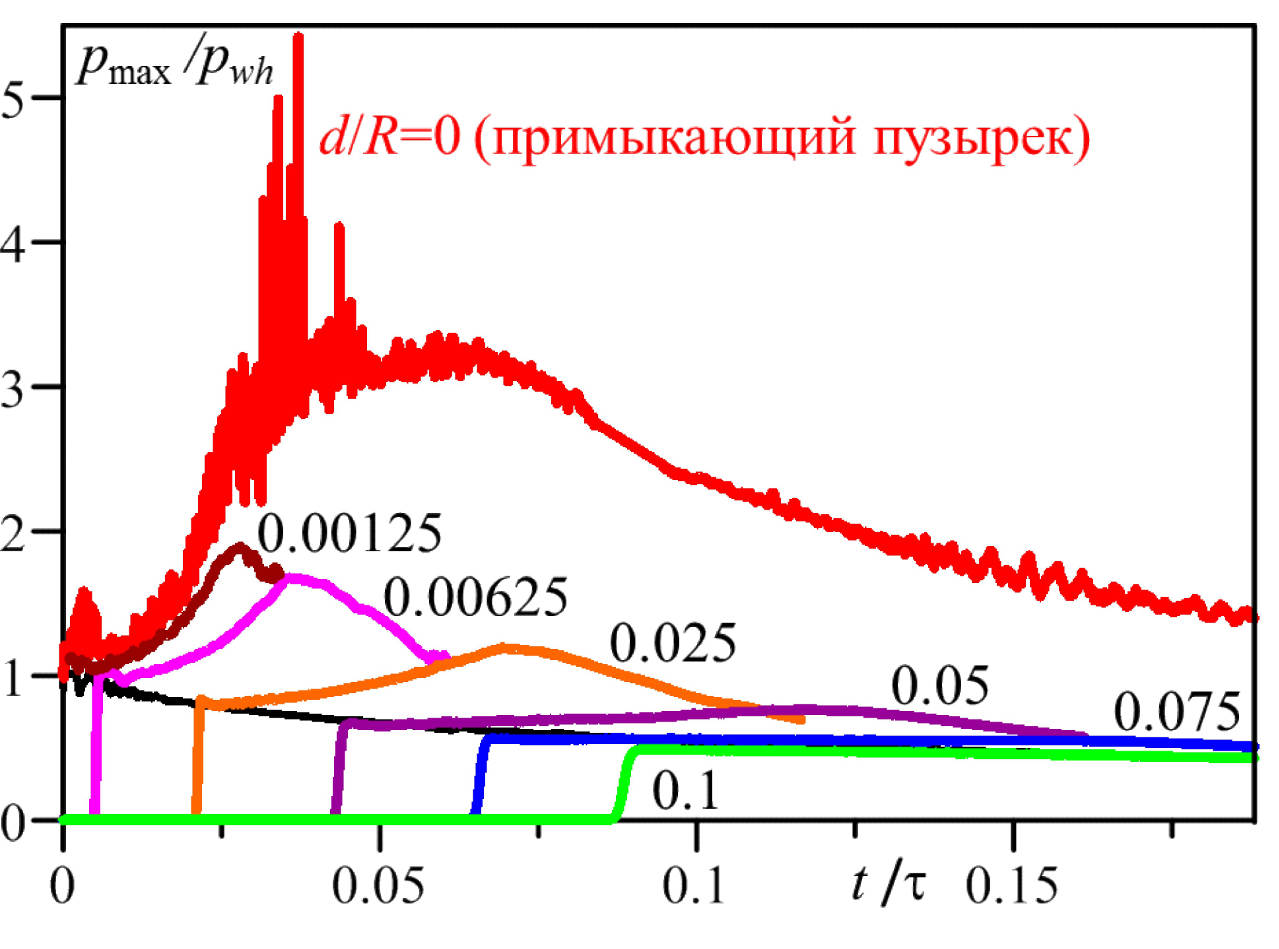
|
Рис.8. Изменение максимума даления на стенке и давления в центре области удара (черная кривая) при воздействии на стенку высокоскоростной струи при наличии на стенке прослойки жидкости разной толщины, τ = R/Cs (Cs – скорость звука в жидкости).
|
7. Разработана методика расчета динамики приповерхностной области металлического тела при заданном законе нагружения. Тело - изотропное идеальное упруго-пластическое, деформации и перемещения малы. Динамика тела описывается линейными уравнениями, пластичность учитывается с использованием условия Мизеса.
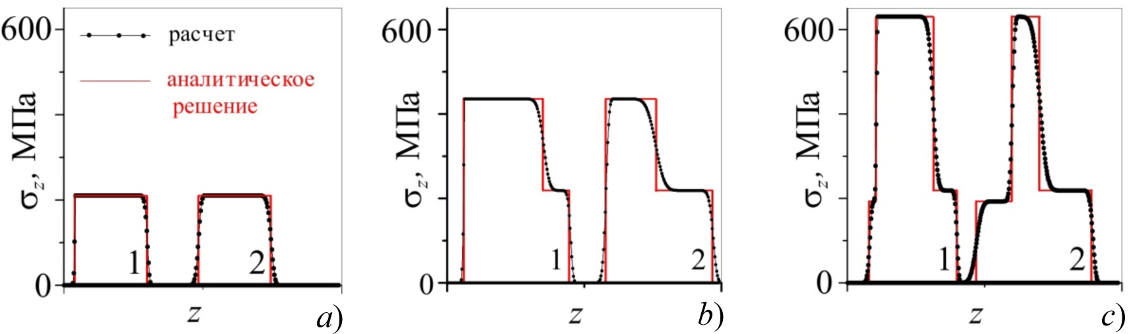
|
Рис. 9. Распространение в теле импульсов продольных напряжений σz в два момента времени (кривые 1 и 2): (a) – без превышения предела текучести материала, (b) – с превышением предела текучести в переднем фронте импульса, (c) – с превышением предела текучести в переднем и заднем фронтах импульса.
|
8. Исследована динамика приповерхностного слоя металлического тела при приложении нему нагрузки, характерной для удара кумулятивной струи, образующейся при схлопывании пузырька у поверхности тела, а также при различных аппроксимациях и упрощениях такой нагрузки [11, 24-28]. Показано, что
- наибольшие напряжения возникают как на поверхности тела, так и на удалении от нее порядка радиуса круговой области нагружения [24, 25].
- предельная интенсивность напряжений в теле (на уровне предела текучести) достигается при значительно (примерно в два раза) меньших скоростях струи, чем в соответствующем одномерном приближении [27].
- наибольшее влияние на величину напряжений и остаточных деформаций из характеристик материала тела (модуль Юнга, коэффициент Пуассона, плотность, предел текучести) оказывает модуль Юнга (в частности, чем больше значение модуля Юнга, тем меньше глубина вмятины), а наименьшее – его плотность [28].
Для тел из алюминиевого и никелевого сплавов при различных скоростях струи определены размеры и конфигурация зон, где возникали напряжения с предельной интенсивностью [26, 27].

|
Рис.10. Поле интенсивности напряжений в теле σz (a) в один из моментов его нагружения по закону, характерному для удара кумулятивной струи, образующейся при схлопывании пузырька у поверхности тела, и, более подробно, соответствующая деформация его поверхности (b, масштаб тела по вертикальной оси увеличен в 104 раз). На рис.10a черная линия – граница области со значениями на уровне предела текучести.
|
9. Установлены закономерности динамики пузырьков около локальных неровностей (осесимметричных выпуклостей и вогнутостей) на плоской твердой стенке в режиме формирования направленной к стенке кумулятивной струи жидкости. Определено влияние параметров неровности стенки на характеристики динамики пузырьков (скорость и радиус конца струи, давление в пузырьке и др.) в тот момент, когда струя бьет по ближней к стенке части поверхности пузырька. Эти характеристики во многом определяют важный для приложений разрушительный потенциал кавитации. Выявлены зависимости этих характеристик от радиуса неровной части стенки, глубины вогнутости и высоты выпуклости. Показано (рис. 10), что с изменением радиуса выпуклой части стенки форма пузырька в момент удара струи изменяется очень сильно: возникают профили со встречно направленной струей, с газовой микрополостью перед бьющим концом струи и с относительно большой областью удара.

|
Рис. 10. Фрагменты профилей локальных выпуклостей на плоской стенке (черные линии) и контуры пузырьков в начале их расширения (синие кружки), в конце расширения (пунктирные линии) и в момент удара кумулятивной струи жидкости по ближней к стенке части поверхности пузырька (красные линии). Стрелкой указано направление удара струи.
|
Основные публикации
- Аганин А.А., Гусева Т.С., Косолапова Л.А., Малахов В.Г., Хисматуллина Н.А. Моделирование импульсного воздействия кавитационных пузырьков на тело // Изв. УНЦ РАН. № 2. 2014. С. 53-61.
- Косолапова Л.А., Малахов В.Г., Хисматуллина Н.А. Ударное воздействие кавитационного пузырька на упругое полупространство // Аналитическая механика, устойчивость и управление. Тр. X Междунар. Четаевской конф. Т.2. Устойчивость. Казань, 12-16 июня 2012г. – Казань: Изд-во Казан. гос. техн. ун-та, 2012. С. 294-304.
- Аганин А.А., Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Схлопывание кавитационного пузырька в жидкости вблизи твердой стенки // Вестник Башкир. ун-та. 2013. Т. 18. Вып. 1. С. 15−21.
- Косолапова Л.А., Малахов В.Г. Численное исследование динамики сфероидальных кавитационных пузырьков вблизи жесткой стенки // Сеточные методы для краевых задач и приложения. Мат. X межд. конф. Казань, 24-29 сентября 2014г. – Казань: Изд-во Казан. ун-та, 2014. С. 429-434.
- Аганин А.А., Гусева Т.С., Косолапова Л.А., Малахов В.Г. Ударные волны в жидкости при импульсном воздействии кавитационного пузырька на жесткую стенку. // Учëн. зап. Казан. ун-та. Т.157. № 2. Сер. Физ.-матем. науки. 2015. С. 5–19.
- Аганин А.А., Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Несферическое схлопывание кавитационного пузырька у стенки с переходом в тороидальную фазу // Известия уфимского научного центра РАН. 2015. №3. С. 5-11.
- Аганин А.А., Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Динамика кавитационного пузырька вблизи твердой стенки // Теплофизика и аэромеханика, 2016. (в печати)
- Аганин А.А., Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Коллапс кавитационного пузырька у твердой стенки // Авиационная техника. Изв. высш. учеб. заведений, 2016. (в печати)
- Гусева Т.С. Воздействие струи, образующейся при схлопывании кавитационного пузырька, на жесткую стенку // Материалы XI Всероссийского съезда по фундаментальным проблемам теоретической и прикладной механики, Казань, 20-24 августа, 2015. С. 1112-1114.
- Аганин А.А., Гусева Т.С., Хисматуллина Н.А. Численное моделирование ударного воздействия высокоскоростной струи на твердое тело // Учен. зап. Казан. ун-та. Сер. Физ.-матем. науки. 2015. Т.157. Кн.1. С. 75-90.
- Аганин А. А., Гусева Т. С. Методика расчета волн в жидкости и газе методом CIP-CUP с применением динамически-адаптивных Soroban-сеток // Вестник Башк. ун-та. Т.19. № 2. 2014. С. 368-380.
- Аганин А.А., Гусева Т.С. Численное моделирование динамики неоднородных сжимаемых сред на основе метода CIP-CUP на адаптивных Soroban-сетках // Учен. зап. Казан. ун-та. Сер. Физ.-матем. науки. 2014. Т.156. Кн.2. С. 55-71.
- Аганин А.А., Гусева Т.С. Расчет волн в жидкости и газе методом CIP-CUP с применением динамически-адаптивных Soroban-сеток // Сеточные методы для краевых задач и приложения. Материалы X междунар. конф. Казань, 24-29 сентября 2014г. – Казань: Изд-во Казан. ун-та, 2014. С. 52-58.
- Аганин А.А, Гусева Т.С. Расчет волн в средах с контактными границами на адаптивных soroban-сетках // 5-ая Международная научная школа молодых ученых "Волны и вихри в сложных средах", Москва: Сборник материалов школы. – М.: МАКС Пресс, 2014. С. 102-105.
- Аганин А.А., Гусева Т.С. Расчет контактного взаимодействия сжимаемых сред без явного выделения межфазных границ // Вестник Башкирского Университета. Т.18. № 3. 2013. С. 646-661.
- Аганин А.А., Гусева Т.С. Численное моделирование контактного взаимодействия сжимаемых сред на эйлеровых сетках // Учен. зап. Казан. ун-та. Сер. Физ.-мат. н. 2012. Т.154. Кн.4. С. 74-99.
- Аганин А.А., Гусева Т.С. Эффект слабой сжимаемости жидкости при взаимодействии пузырьков в сильных акустических полях // МЖГ. 2010. № 3. С.3-16.
- Малахов В.Г., Хисматуллина Н.А. Динамика упругого тела под действием нагрузки, характерной для удара струи жидкости // Вестник Нижегородского университета им. Н.И. Лобачевского, №4. Часть 4. – Н. Новгород: Изд-во ННГУ им. Н.И. Лобачевского, 2011. С. 1597-1599.
- Аганин А.А., Ильгамов М.А., Малахов В.Г., Халитова Т.Ф., Хисматуллина Н.А. Ударное воздействие кавитационного пузырька на упругое тело // Ученые записки Казанского университета. 2011. Т.153. Кн.1. С. 131-146
- Аганин А.А., Ильгамов М.А., Хисматуллина Н.А. Упруго-пластические деформации в теле при ударном воздействии кавитационного пузырька // Ученые записки Казан. ун-та. Т.155. Кн.2. 2013. С. 131-143
- Аганин А.А., Хисматуллина Н.А. Ударное воздействие струи жидкости на упруго-пластическое тело //Ученые записки Казанского университета. Т.156. Кн.2. 2014. С. 72-86
- Аганин А.А., Ильгамов М.А., Хисматуллина Н.А. Деформация поверхности тела при ударе водяной струи // Известия Уфимского научного центра РАН. 2015. №3. С. 12-18.
- Аганин А.А., Гусева Т.С., Косолапова Л.А., Малахов В.Г. Ударные волны в жидкости при импульсном воздействии кавитационного пузырька на жесткую стенку // Ученые записки Казанского университета. Сер. Физ.-мат. науки. 2015. Том 157. Кн. 2. С. 5-19. (ВАК)
- Аганин А.А., Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Несферическое схлопывание кавитационного пузырька у стенки с переходом в тороидальную фазу//Изв. УНЦ РАН. 2015. №3. С.5-11.
- Аганин А.А., Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Динамика кавитационного пузырька вблизи твердой стенки //Теплофизика и аэромеханика. 2016. Т.23. №2. С. 219-228.
- Аганин А.А., Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Коллапс сфероидального кавитационного пузырька у твердой стенки //Изв. вузов. Авиационная техника. 2016. №2. С. 32-37.
- Аганин А.А., Гусева Т.С. Удар струи по тонкому слою жидкости на стенке // Вестник Башкирского ун-та. Т.21. № 2. 2016. С. 245-251.
- Аганин А. А., Гусева Т. С. Удар жидкого конуса по плоской жесткой стенке // Учен. зап. Казан. ун-та. Сер. Физ.-матем. науки 2016. Том 158, № 1, С. 117-128.
- Аганин А.А., Хисматуллина Н.А. Модификации метода С.К. Годунова для расчета распространения возмущений в упругом теле // Труды ин-та механики им. Р.Р. Мавлютова УНЦ РАН. 2016. Т. 11. С. 119–126. Текст
- Аганин А.А., Ильгамов М.А., Хисматуллина Н.А. Зависимость динамики приповерхностного слоя тела от особенностей его нагружения при ударе струи жидкости // Изв. УНЦ РАН. 2016. №3. С. 5-14.
- Aganin A. A., Khismatullina N. A. Features of deformation of metal body surfaces under impact of a water jet // Journal of Physics: Conference series 669. 2016. 012031.
- Aganin A.A., Guseva T.S. Numerical simulation of liquid jet impact on a rigid wall // XI International Conference “Mesh Methods for Boundary-Value Problems and Applications”. Journal IOP Conference Series: Materials Science and Engineering. 2016. V. 158. 012004.
- Aganin A.A., Guseva T.S., Kosolapova L.A., Khismatullina N.A. The calculation of weakly nonspherical cavitation bubble impact on a solid // XI Intern. Conference “Mesh Methods for Boundary-Value Problems and Applications”. J. IOP Conf. Series: Materials Science and Engineering. 2016. V. 158. 012003.
- Аганин А.А., Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Динамика пузырька газа в жидкости у твердой стенки. // Актуальные проблемы сплошной среды. К 25-летию ИММ КазНЦ РАН. Сборник научных трудов. – Казань: Изд-во «Фэн» АН РТ, 2016. С. 61-84.
- Аганин А.А., Гусева Т.С. Моделирование удара струи по стенке // Актуальные проблемы механики сплошной среды. К 25-летию ИММ КазНЦ РАН. Сборник научных трудов. Ка-зань: Изд-во «Фэн» АН РТ, 2016. С. 165-192.
- Аганин А.А., Хисматуллина Н.А. Динамика приповерхностного слоя тела при ударе струи жидкости // Актуальные проблемы механики сплошной среды. К 25-летию ИММ КазНЦ РАН. Сборник научных трудов. Казань: Изд-во «Фэн» АН РТ, 2016. С. 193-206.
- Аганин А.А., Гусева Т.С. Численное моделирование удара струи по стенке // Мат. моделирование. 2017. Т.29. №3. С.123-138.
- Аганин А.А., Косолапова Л.А., Малахов В.Г. Численное моделирование эволюции пузырька газа в жидкости вблизи твердой стенки // Мат. моделирование. 2017. Т.29. №7. С.15-28.
- Аганин А.А., Гусева Т.С., Косолапова Л.А. Воздействие кавитационного пузырька на стенку // Изв. вузов. Авиационная техника. 2017. № 3. С. 67-72.
- Аганин А.А., Гусева Т.С. Влияние формы конца струи при ее ударе по поверхности жидкости // Ученые записки Казанского ун-та. Сер. Физ.-матем. Науки. 2017. Том 159. Книга 2. С. 135-142.
- Аганин А.А., Хисматуллина Н.А. Расчет двумерных возмущений в упругом теле //Ученые записки Казанского университета. Сер. Физ.- матем. Науки. 2017. Т.159. Книга 2. С.143-160.
- Аганин А.А., Хисматуллина Н.А. Схемы второго порядка точности для расчета динамики возмущений в упругом теле // Труды ин-та механ. им.Р.Р. Мавлютова УНЦ РАН. 2017. Т. 12. № 1. С. 44–50.
- Аганин А.А., Гусева Т.С., Хисматуллина Н.А. Зависимость воздействия кавитационного пузырька на тело от формы возникающей при его коллапсе струи // Изв. Уфим. науч. цент. РАН. 2018. № 3. С. 5–12.
- Ильгамов М.А., Косолапова Л.А., Малахов В.Г. Динамика пузырька газа в жидкости у стенки на тороидальной фазе движения // Изв. Уфим. науч. цент. РАН. 2018. №3. С. 13–21.
- Аганин А.А., Хисматуллина Н.А. Эффективность TVD-модификации метода С. К. Годунова при расчете волн в упруго-пластическом теле // Вест. Башкир. ун-та. 2018. Т. 23. № 3. С. 655–660.
- Аганин А.А., Хисматуллина Н.А. Расчет волн в упруго-пластическом теле // Учен. зап. Казан. ун-та. Сер. физ.-мат. науки. 2018. Т.160. Кн.3. С. 435–447.
- Aganin A.A., Guseva T.S. Effect of wetting a wall on the impact of a liquid jet // Journal of Physics: Conference series. 2018. 1058: 012070.
- Aganin A.A., Kosolapova L.A., Malakhov V.G. The evolution of a gas bubble in a liquid near a flat wall // Journal of Physics: Conference series. 2018. 1058: 012069.
- Аганин А.А., Гусева Т.С. Влияние формы конца струи жидкости на ее удар по сухой стенке // Учен. зап. Казан. ун-та. Сер. Физ.-мат. науки. 2019. Т. 161. № 1. С. 39‒52.
- Аганин А.А., Гусева Т.С., Косолапова Л.А., Хисматуллина Н.А. Зависимость воздействия кавитационного пузырька на тело от давления жидкости // Учен. зап. Казан. ун-та. Сер. Физ.-мат. науки. 2019. Т. 161. №. 2. С. 165–180.
- Aganin A.A. Khismatullina N.A. UNO Modifications of the Godunov Method for Calculating the Dynamics of an Elastic-Plastic Body // Lobachevskii Journal of Mathematics. 2019. Vol. 40. Iss. 3. P. 256‒262.
- Guseva T.S., Malakhov V.G. Effect of Liquid Compressibility at a Jet Impact on a Wall // Lobachevskii Journal of Mathematics. 2019. Vol. 40. Iss. 6. P. 757‒762.
- Khismatullina N. A. Liquid jet impact on the surface of metal alloys // Lobachevskii Journal of Mathematics. 2019. Vol. 40. Iss. 6. P. 763‒768.
- Aganin A., Guseva T. Numerical simulation of liquid mass collision with a wall // Progress in Computational Fluid Dynamics, An International Journal. 2019. Vol. 19. No. 5. P. 293–306.
- A. A. Aganin, T. S. Guseva, L. A. Kosolapova, and V. G. Malakhov, Dynamics of an Acoustically Excited Gas Cavity Attached to a Rigid Surface // Lobachevskii Journal of Mathematics. 2019. Vol. 40. Iss. 11. P. 1897–1903.
- Aganin A.A., Khismatullina N.A. UNO and TVD schemes for calculation of waves in an elastic- plastic body // Journal of Physics: Conference series. 2019. 1328: 012001
- Aganin A.A., Kosolapova L.A., Malakhov V.G. Dynamics of a Spheroidal Gas Bubble near a Rigid Surface // Journal of Physics: Conference series. 2019. 1328: 012043.
- Аганин А. А., Ильгамов М. А., Гусева Т. С. Влияние формы головной части струи на ее удар по смоченной стенке // ПМТФ. 2019. Т.60. № 4. С. 61–67 {A. A. Aganin, M. A. Il’gamov, T. S. Guseva, Influence of the Shape of the Jet Head on its Impact on a Wetted Wall // Journal of Applied Mechanics and Technical Physics. 2019. Vol. 60. No. 4. P. 644 – 649.
- A. A. Aganin, L. A. Kosolapova and V. G. Malakhov Numerical investigation of the liquid motion influence on the collapse of a cavitation bubble near a wall // Journal of Physics: Conference series. 2019. 1158(2): 022006.
- Аганин А.А., Ильгамов М.А., Мустафин И.Н. Ударная кавитация жидкости в цилиндрической емкости // Ученые записки Казан. университета. Сер. Физ.-мат. науки, 2020. Т. 162. № 1. С. 27 - 37.
- Aganin A. A., Guseva T.S., Khismatullina N. A. Influence of a Liquid Film Covering a Solid on Liquid Jet Impact Against its Surface // Lobachevskii Journal of Mathematics, 2020. V. 41. № 12. P. 2621 - 2627.
- Khismatullina N. A. Calculation of Waves in an Elastic-Plastic Body Based on ENO Modifications of the Godunov Method // Lobachevskii Journal of Mathematics, 2020. V. 41. № 7. P. 1228 - 1234.
- Kosolapova L. A., Malakhov V. G. Influence of the Initial Shape of a Gas Bubble on its Dynamics near a Wall under Acoustic Excitation // Lobachevskii Journal of Mathematics, 2020. V. 41. № 7. P. 1235 - 1241.
- Аганин А.А., Гусева Т.С., Косолапова Л.А., Малахов В.Г. Динамика пузырька и импульсное нагружение твердой поверхности при акустическом воздействии // Ученые записки Казан. Университета.. Сер. Физ.-мат. науки, 2021. Т. 163. № 1. С. 31 - 47.
- Гусева Т.С. Ударное воздействие струи жидкости на смоченную стенку // Ученые записки Казан. университета Сер. Физ.-мат. науки, 2021. Т. 163. № 2. С. 117 - 127.
- Aganin A.A., Kosolapova L.A., Malakhov V.G. Numerical study of the dynamics of a gas bubble near a wall under ultrasound excitation // Lobachevskii Journal of Mathematics, 2021. V. 42. № 1. P. 24 - 29.
- Guseva T. S. The initial stage of a liquid drop impingement onto a curved surface // Lobachevskii Journal of Mathematics, 2021. V. 42. № 9. P. 2144 - 2150.
- Kosolapova L. A. Dynamics of a Gas Bubble near a Wall under Acoustic Excitation with the Formation of Cumulative Jet // Lobachevskii Journal of Mathematics, 2021. V. 42. № 9. P. 2159 - 2164.
- Malakhov V.G. Modeling of the dynamics of a gas bubble in liquid near a curved wall // Lobachevskii Journal of Mathematics, 2021. V. 42. № 9. P. 2165 - 2171.
- Aganin A.A. High-speed liquid impact on a liquid surface and a wetted wall // Lobachevskii Journal of Mathematics, 2022. V. 43. № 8. P. 2029 - 2045.
- Aganin A.A. High-Speed Liquid Impact Onto a Solid Surface // Lobachevskii Journal of Mathematics, 2022. V. 43. № 10. P. 195 - 205.
- Aganin A., Kosolapova L., Malakhov V. Bubble dynamics near a locally curved region of a plane rigid wall // Physics of Fluids. 2022. V.34. 097105.
- Kosolapova L.A., Malakhov V.G. Expansion and collapse of a bubble near a cylindrical protuberance on a plane wall// Lobachevskii Journal of Mathematics. 2022. V. 43. P. 1145–1151.
- Aganin A. A., Kosolapova L. A., Malakhov V.G. Collapse of a Toroidal Cavity in Liquid near a Wall // Lobachevskii Journal of Mathematics, 2023. V. 44. № 5. P. 1558 - 1563.
- Guseva T.S. Analysis of the high-speed liquid impact onto a curved liquid surface with Heymann’s theory // Lobachevskii Journal of Mathematics, 2023. V. 44. № 5. P. 1661 - 1670.
- Guseva T. S. Jet impact during bubble collapse near a local bump on a solid wall // Lobachevskii Journal of Mathematics, 2024. V. 45. № 5. P. 2015 - 2025.
|



