Одной из важных особенностей динамики пузырьков в жидкости является возможность реализации сжатия содержимого пузырьков с достижением высоких давлений, плотностей и температур. Среди явлений, в которых термодинамические параметры достигают экстремально больших значений, можно отметить периодическую однопузырьковую сонолюминесценцию, явление выхода нейтронов и ядер трития при акустической кавитации дейтерированного ацетона, кавитационный синтез наноалмазов в бензоле и толуоле.

1. Периодическая однопузырьковая сонолюминесценция. Под этим явлением подразумевается свечение одиночного пузырька (рис. 1) при акустических колебаниях в жидкости. Согласно уже вполне устоявшемуся мнению явление однопузырьковой сонолюминесценции является результатом достижения очень высоких уровней термодинамических параметров внутри пузырька вблизи момента наиболее сильного сжатия.

Рис. 1. Периодическая однопузырьковая сонолюминесценция: свечение газового пузырька в центре стеклянной колбы с жидкостью (Flannigan D.J., Suslick K.S. // Nature Physics. 2010. V. 6. P. 598-601).

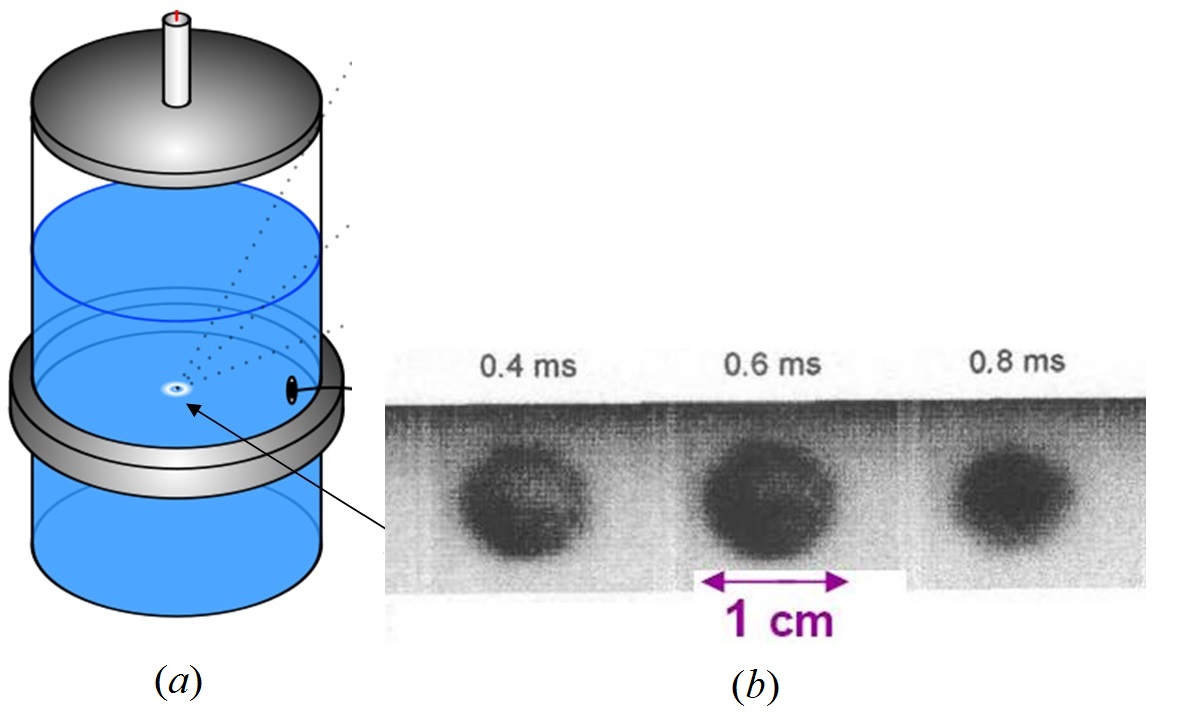
2. Нейтронная эмиссия при акустическом возбуждении кластера кавитационных пузырьков в дейтерированном ацетоне – «Пузырьковый термояд». В центре колбы с жидким дейтерированным ацетоном в стоячей волне давления (рис. 2a) испытывает акустические колебания кластер кавитационных пузырьков (рис. 2b). В моменты экстремального сжатия пузырьков наблюдается выход термоядерных нейтронов и ядер трития (Taleyarkhan R.P., West C.D., Cho J.S., Lahey R.T. (Jr), Nigmatulin R.I., Block R.C. // Science. 2002. V. 295. P. 1868-1873).

Рис. 2. Схема экспериментальной установки для получения нейтронной эмиссии при акустической кавитации дейтерированного ацетона (a); сферический кластер кавитационных пузырьков (b) (Xu Y., Butt A. // Nuclear Engineering and Design. 2005. V. 235. P. 1317-1324).

3. Производство наноразмерных алмазов при акустической кавитации бензола и толуола. В колбе с жидким бензолом или толуолом большое количество кавитационных пузырьков подвергается сжатию бегущей ударной волной огромной амплитуды. В момент экстремального сжатия пузырьков из-за огромных давлений имеющийся в молекулах бензола или толуола углерод организуется в алмазные структуры нанометровых размеров (Галимов Э.М. и др. // Доклады Академии наук. 2004. Т. 395, № 2. С. 187-191).

Рис. 3. Схема экспериментальной установки для синтеза наноалмазов. При плавном движении поршней (заштрихованные элементы) вправо в жидкости появляется множество кавитационных пузырьков; при резком ударном движении правого поршня влево организуется бегущая ударная волна через пузырьковую жидкость.

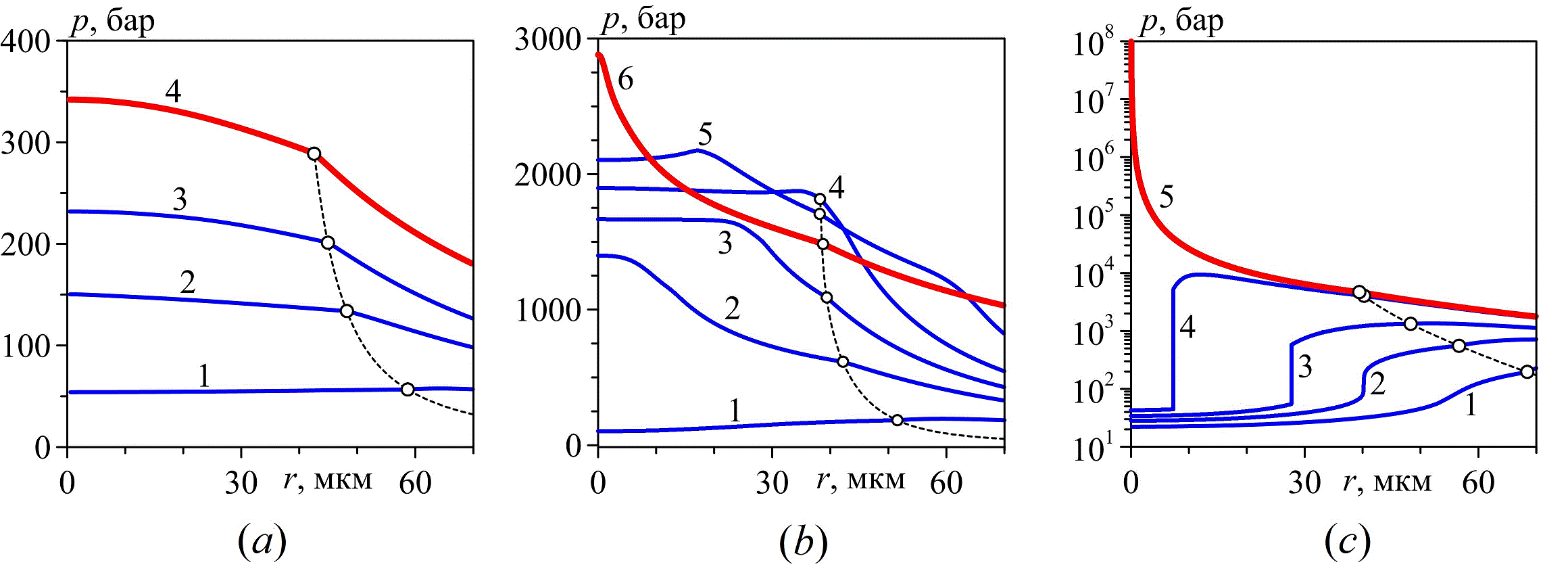
1. Выполнено исследование сильного (взрывного) сжатия (коллапса) в жидкости (воде и ацетоне) сферического кавитационного (парового) пузырька [9]. Давление жидкости p₀ варьируется в диапазоне от 1 до 100 бар, начальный радиус пузырька равен 500 мкм, температура воды 20^°С, ацетона 0 и 20^°С, пар в пузырьке в начале сжатия находится в состоянии насыщения. Показано, что с ростом p₀ последовательно реализуются однородное сжатие (рис. 4a), сжатие простыми волнами (рис. 4b), сжатие ударными волнами (рис. 4c). Наиболее высокие значения параметров будут достигаться при третьем сценарии. В случае пузырька в ацетоне сценарии сжатия меняются намного быстрее. В результате в этом случае все сценарии реализуются уже при p₀ ≤ 3.5 бар, тогда как в случае пузырька в воде при p₀ < 100 бар сценарий, проиллюстрированный на рис. 4c, не реализуется. По той же причине при больших p₀ (≥ 10 бар) степень сжатия среды пузырька в ацетоне намного больше, чем пузырька в воде, хотя при малых p₀ (≤ 1 бар) это соотношение противоположно.

Рис. 4. Радиальное распределение давления при сжатии пара в пузырьке в ацетоне близком к однородному (a, давление жидкости p0 = 1 бар), при сжатии пара в пузырьке за счет радиального схождения и фокусировки простых (b, p0 = 2 бар) и ударных (с, p0 = 15 бар) волн сжатия (начальный радиус пузырька 0.5 мм, температура ацетона 20°С). Координата r = 0 соответствует центру пузырька; кружки – граница пузырька (слева – пар, справа – жидкость).

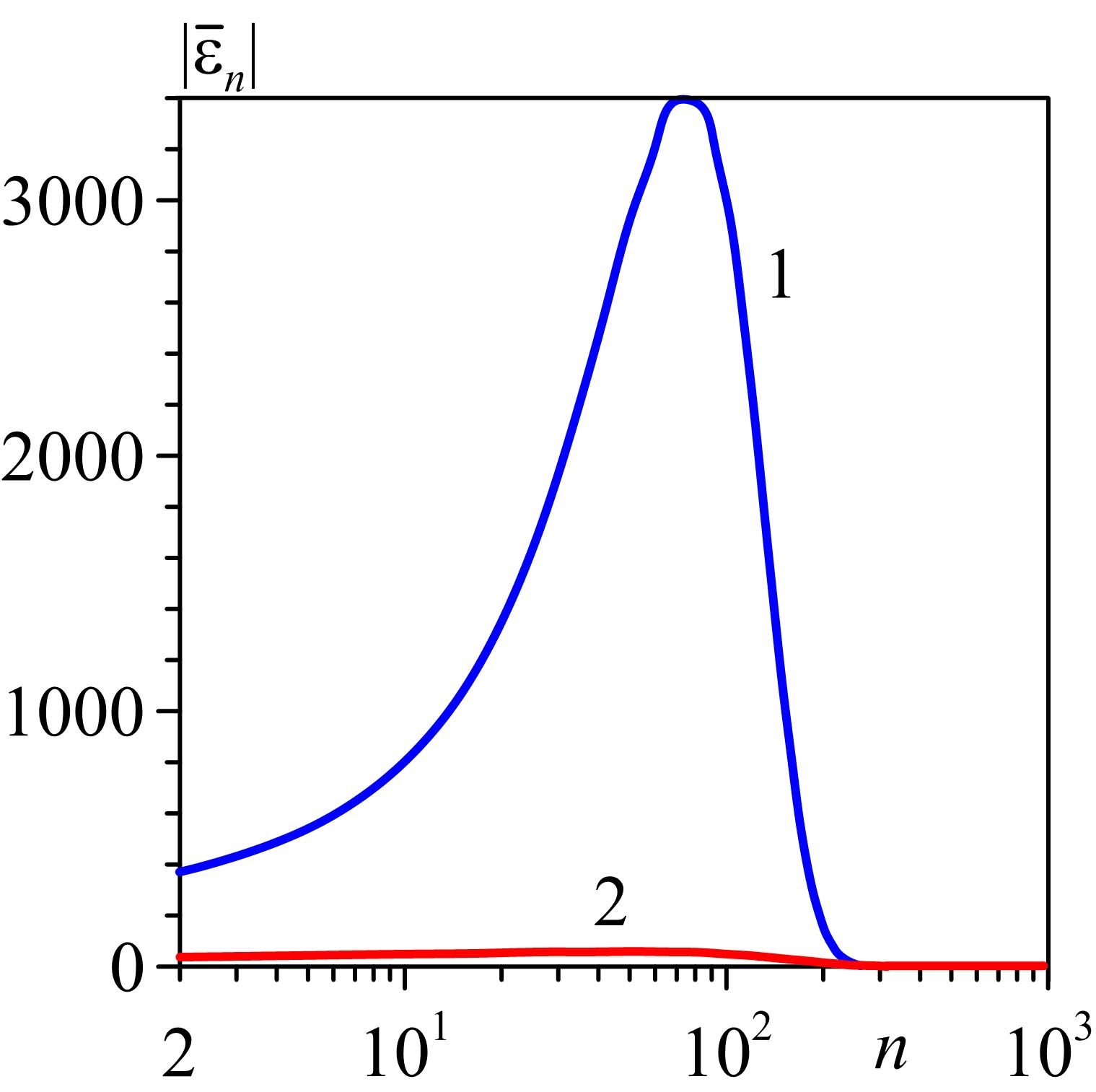
2. Установлено, что при сжатии пузырька с начальным радиусом 0.5 мм при давлении жидкости 15 бар и ее температуре 20^°С амплитуда возмущений сферичности пузырька, отнесенная к его текущему радиусу, может возрастать к концу его сжатия до 3400 раз в воде и только в 70 раз в ацетоне.

Рис. 5. Зависимость 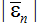(отношения амплитуды безразмерного возмущения сферичности пузырька в виде сферической гармоники степени n в конце сжатия пузырька к ее начальному значению) от n для воды (кривая 1) и ацетона (кривая 2).

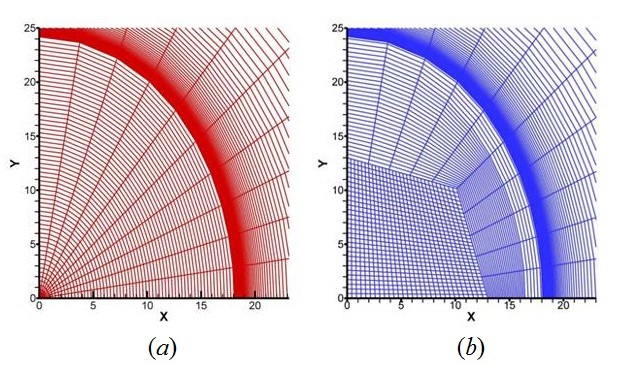
3. Разработана методика численного исследования финальной стадии фокусировки радиально сходящейся несферической ударной волны в окрестности центра осесимметричного кавитационного пузырька, подвергнутого сильному сжатию [12]. В используемой гидродинамической модели учитываются сжимаемость жидкости, теплопроводность пара и жидкости, испарение и конденсация на межфазной поверхности, применяются реалистичные широкодиапазонные уравнения состояния. Сетки подвижные, с явным выделением поверхности пузырька (рис. 6a). Методика основана на TVD-модификации схемы Годунова второго порядка точности по пространству и времени. Ее экономичность обусловлена учетом особенностей задачи в финальной стадии фокусировки несферической ударной волны в центральной области пузырька. После того, как ударная волна становится сильно несферической, в центральной области пузырька криволинейная радиально-расходящаяся сетка заменяется на прямолинейную косоугольную, близкую к декартовой (рис. 6b). В этот же момент сферическая неподвижная система отсчета сменяется цилиндрической.

Рис. 6. Фрагменты расчетных сеток созданной методики расчета эволюции сильно несферических ударных волн в осесимметричном кавитационном пузырьке при его высокоскоростном сжатии в жидкости в момент замены в центральной области пузырька криволинейной радиально-расходящейся сетки (a) на прямолинейную косоугольную, близкую к декартовой (b). Внутренняя граница сливающихся ячеек сетки – поверхность пузырька.

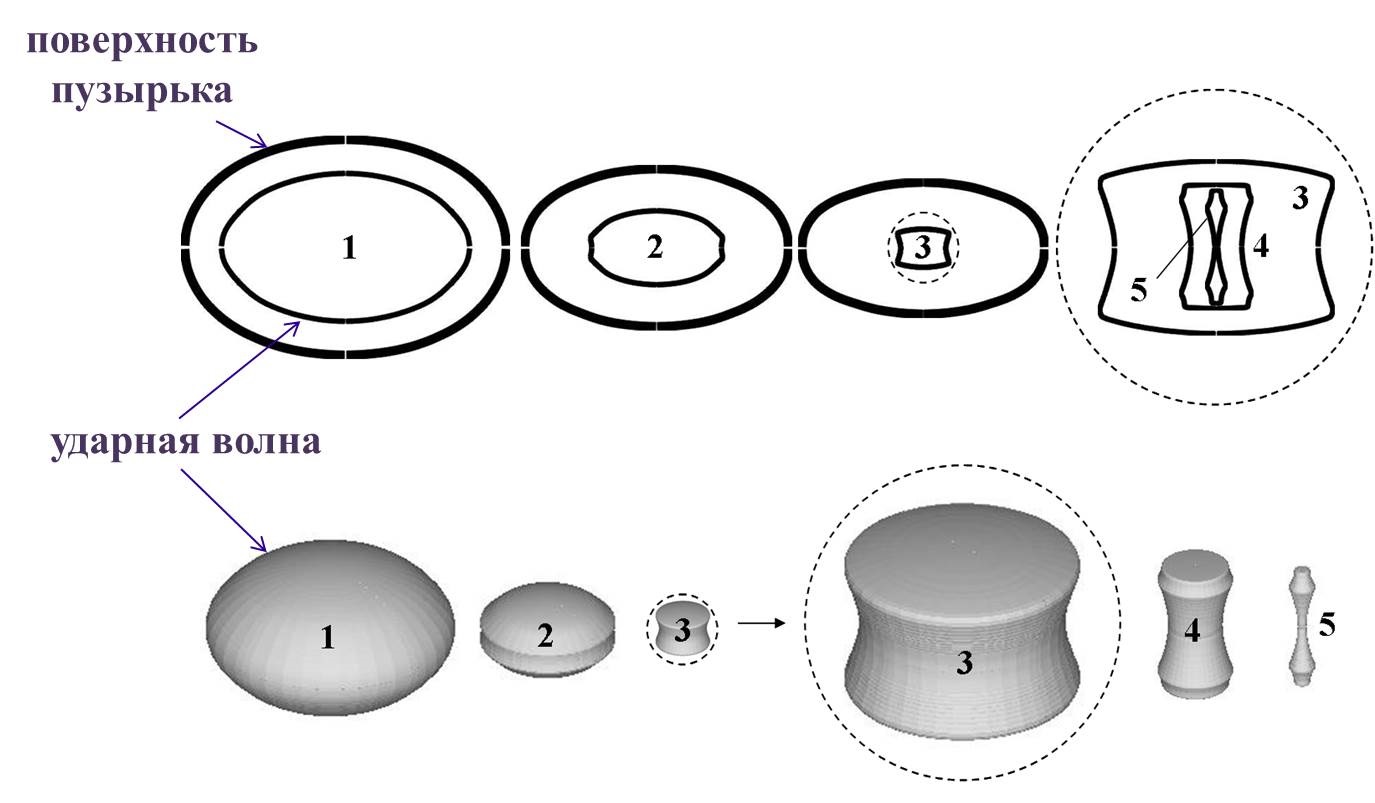
4. Показано, что малые начальные сфероидальные отклонения формы кавитационного пузырька от сферической приводят к снижению степени сжатия среды в нем при его сильном сжатии на режиме с образованием в его полости радиально сходящихся ударных волн. При этом степень сжатия среды в изначально слегка вытянутом пузырьке оказывается больше, чем в изначально слегка сплюснутом. Такая разница связана с различием фокусировки сходящихся ударных волн в этих пузырьках. В случае изначально вытянутого пузырька ударная волна в начале смыкания полости перед ее фронтом приобретает гантелеподобную форму, а случае изначально сплюснутого пузырька становится дискообразной. В результате в отличие от сферической фокусировки в чисто сферическом пузырьке в случае изначально вытянутого пузырька фокусировка ударной волны реализуется близкой к цилиндрической (рис. 7), а в случае изначально сплюснутого пузырька – близкой к столкновению двух плоских ударных волн (рис. 8).

Рис. 7. Контуры поверхности изначально слегка вытянутого (амплитуда безразмерного сфероидального возмущения сферичности пузырька, т.е. в виде сферической гармоники степени 2, ε2 (t = 0) = +0.0033) пузырька в его осевых сечениях в три момента времени 1-3 (внешние сплошные линии) и аналогичные контуры фронта радиально сходящейся ударной волны в его полости в пять моментов времени 1-5 (внутренние сплошные линии) в процессе схождения этой волны (а) и соответствующие контурам 1-5 пять поверхностей ударной волны (б). Штриховой линией проведены характеризующие масштаб окружности r = 7.48 мкм.

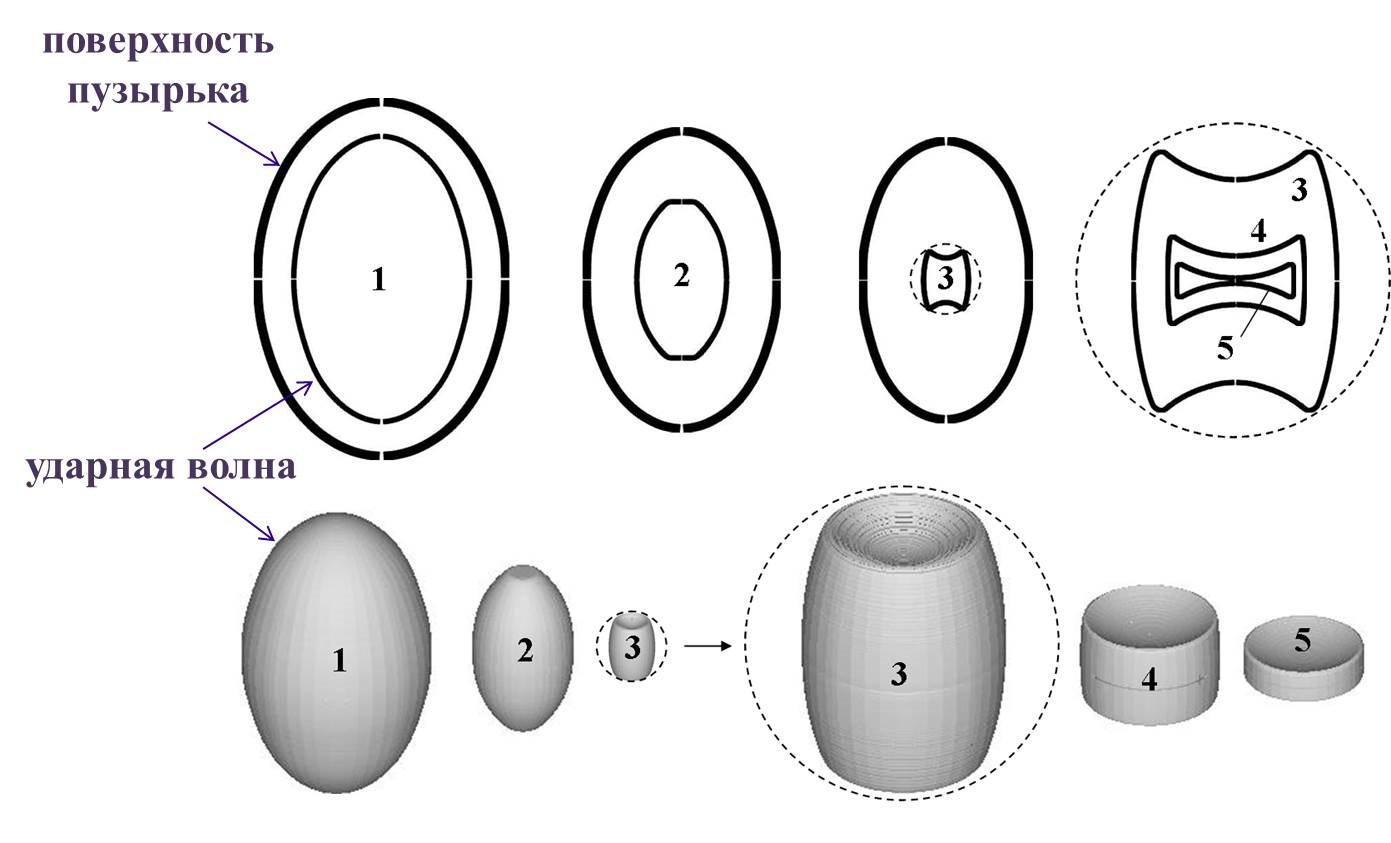
Рис. 8. То же, что и на рис. 7, но для изначально слегка сплюснутого пузырька (ε2 (t = 0) = –0.0033).

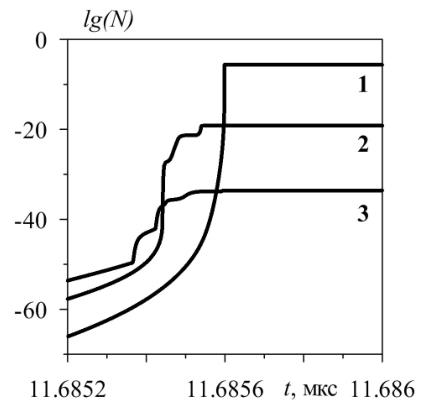
5. Показано, что характеризуемая числом произведенных нейтронов степень сжатия среды в несферических пузырьках меньше, чем в сферическом. При этом при условии одинаковой амплитуды начального возмущения сферичности пузырька количество произведенных нейтронов в изначально слегка вытянутом пузырьке больше, чем в изначально сплюснутом. Степень сжатия среды в пузырьке оценивается с помощью интегральной свертки работы Nigmatulin R.I. et al. Physics of Fluid. 2005. V. 17. 107106, выражающей число образующихся в пузырьке нейтронов на отрезке времени от 0 до t.

Рис. 9. Изменение логарифма от числа произведенных в пузырьке нейтронов N при сжатии изначально сферического (кривая 1), слегка вытянутого (ε2 (t = 0) = +0.0033, кривая 2) и сплюснутого (ε2 (t = 0) = –0.0033, кривая 3) пузырьков.

6. Разработана математическая модель однократного сильного совместного расширения-сжатия расположенных в жидкости в линию слабонесферических кавитационных пузырьков [4, 8]. Учитывается нестационарная теплопроводность в паре и жидкости, неравновесные испарение и конденсация. Применяются широкодиапазонные уравнения состояния, построенные по экспериментальным данным.

На фазе расширения и на наиболее продолжительной низкоскоростной стадии сжатия динамика пузырьков описывается обыкновенными дифференциальными уравнениями относительно радиусов пузырьков, координат их центров и амплитуд их несферичности в виде сферических гармоник [1]. В финальной высокоскоростной стадии сжатия взаимодействие пузырьков не учитывается, движение пара и жидкости расщепляется на сферическую составляющую и ее малое несферическое возмущение [10, 11]. Сферическая составляющая описывается уравнениями газовой динамики, а несферическая – обыкновенными дифференциальными уравнениями относительно амплитуд несферичности пузырьков в виде сферических гармоник.

7. Проведено численное исследование однократного сильного расширения-сжатия расположенных в линию (в виде стримера) кавитационных пузырьков в условиях известных экспериментов по акустическому сверхсжатию пузырьков в дейтерированном ацетоне. Показано, что:
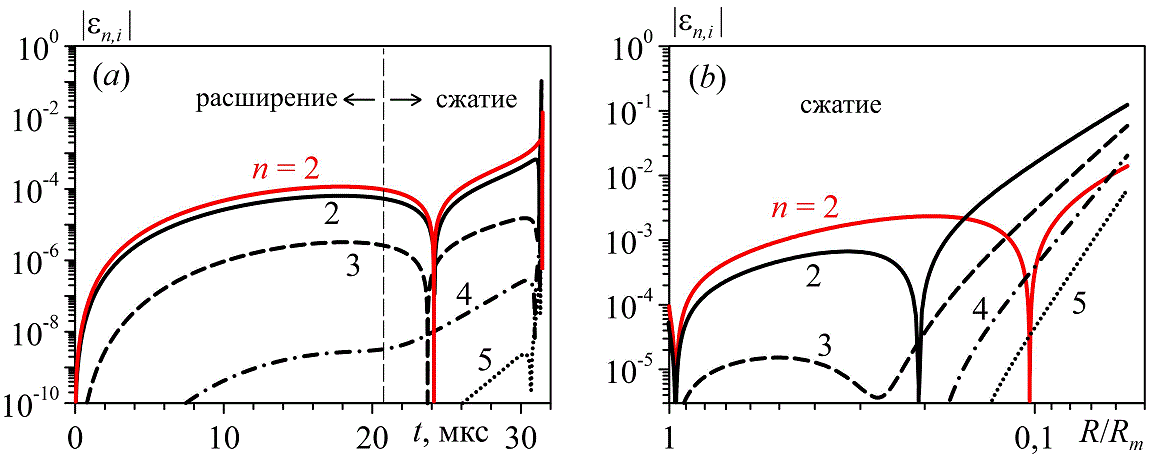
– при расширении более близкие к центру пузырьки деформируются сильнее периферийных, тогда как к концу сжатия ситуация меняется на противоположную (рис. 10);
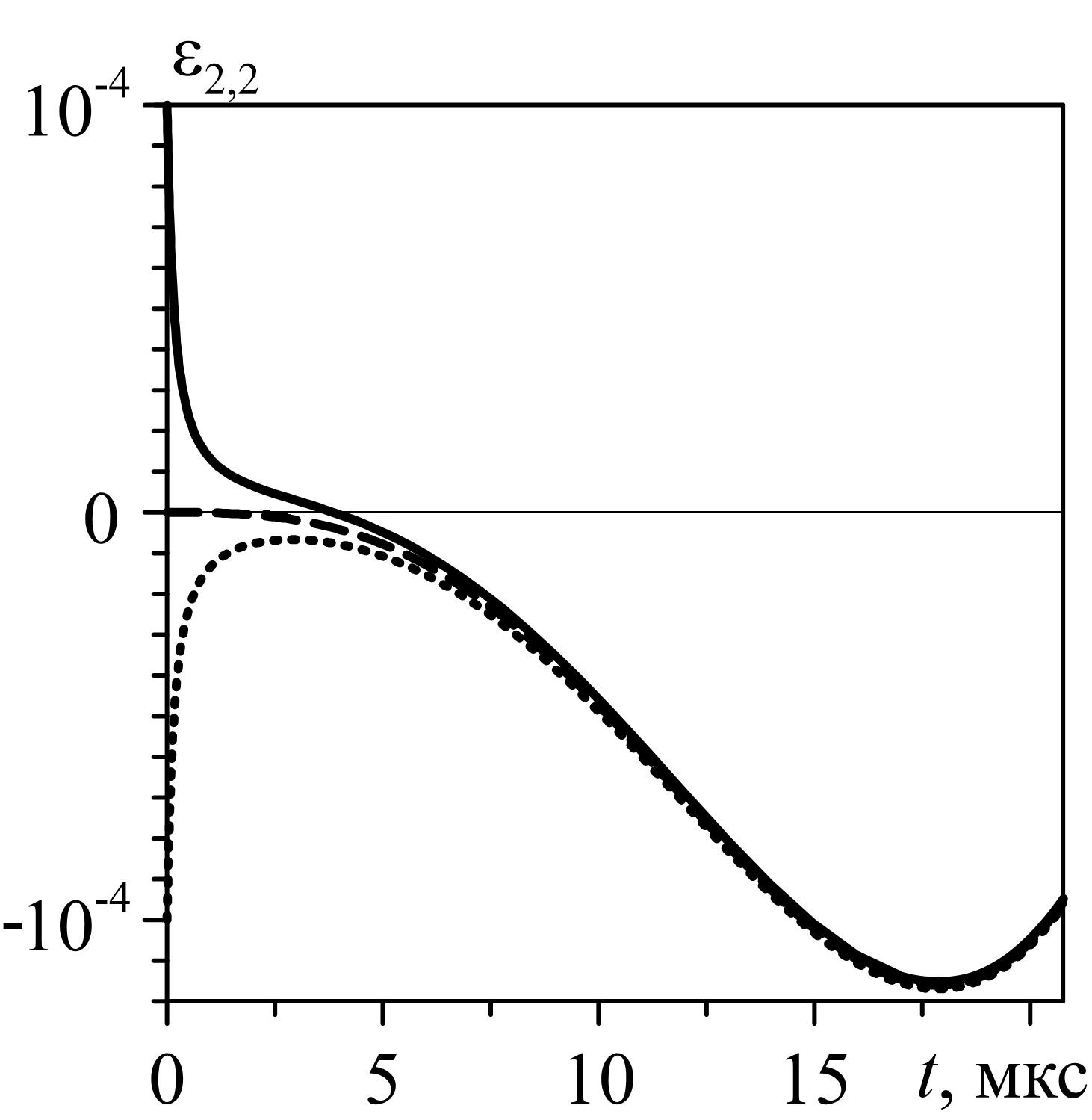
– при произвольной по виду и достаточно малой по величине начальной несферичности пузырьков их форма в конце их совместного расширения (а значит, и в конце сжатия) определяется их взаимодействием (начальная форма «забывается») (рис. 11);
– пузырьки ведут себя как одиночные в финальной высокоскоростной стадии их сжатия, где их поступательное движение на периферии сильно ускоряется, а перемещение в центральной области оказывается незначительным (т.е. центральные пузырьки в конце сжатия деформируются как одиночные неподвижные);
– по мере увеличения числа пузырьков различие их деформаций в центральной области все более уменьшается, так что при достаточно большом их количестве центральные пузырьки деформируются практически одинаково;
– с увеличением расстояния между пузырьками и с уменьшением длины волны возмущений их сферичности деформация пузырьков уменьшается.

Рис. 10. Деформация трех расположенных в линию равноотстоящих пузырьков по гармоникам с номерами n = 2-5 при их расширении и сжатии (a) и, более подробно, при сжатии (b). Красные кривые соответствуют центральному пузырьку (i = 2), черные – боковым (i = 1, 3), d0 / Dmax = 11, d0 – начальное расстояние между соседними пузырьками, Dmax – диаметр пузырьков в конце расширения.

Рис. 11. Изменение ε2,2(t) – амплитуды несферичности по второй гармонике центрального пузырька в группе из трех равноотстоящих пузырьков (d0 / Dmax = 11) в ходе их расширения при ε2,2 (0) = –10–4, 0, 10–4.

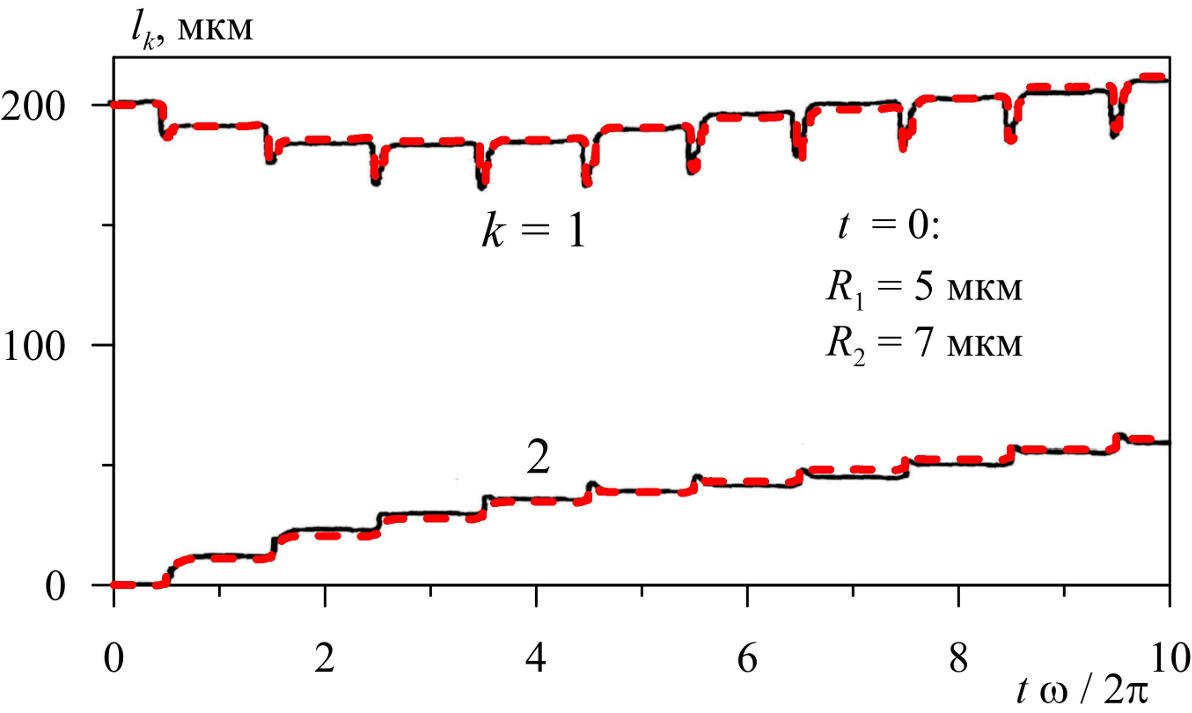
8. Разработана математическая модель пространственного гидродинамического взаимодействия сферических газовых пузырьков в жидкости в акустическом поле. Она представляет собой систему обыкновенных дифференциальных уравнений второго порядка относительно радиусов пузырьков и радиус-векторов их центров. Полученные уравнения имеют четвертый порядок точности относительно R / D, где R – характерный радиус пузырьков, D – характерное расстояние между пузырьками, что на порядок выше точности известных в литературе моделей. Вывод уравнений осуществляется методом сферических функций с использованием интеграла Коши-Лагранжа, кинематических и динамических граничных условий на поверхности пузырьков. При этом эффекты вязкости и сжимаемости жидкости учитываются приближенно, газ в пузырьках полагается гомобарическим.

Рис. 12. Изменение координат центров двух взаимодействующих пузырьков на прямой, проходящей через центры этих пузырьков в начале их взаимодействия. Красные штриховые линии – результаты предложенной трехмерной модели, черные сплошные – результаты осесимметричной модели работы Doinikov A.A. Phys. Rev. E. 2001. V. 64. N 2. 026301. Давление жидкости p∞ = p0 – pa sin ωt, p0 = 1 бар, pa = 1.2 бар, ω/ 2π = 20 кГц.